By Dr Tsanakas, Lecturer in Actuarial Science
Cass Business School
Parameter and model uncertainty are increasingly discussed in the capital modelling community, especially since model-intensive approaches have become standard under ICAS and, soon, Solvency II. Our research addresses a fundamental question for regulators and companies: How can the impact of parameter risk on insurance solvency be assessed and how can it be mitigated?
Financial institutions such as insurance companies are regulated according to a Value-at-Risk principle. This means that they have to hold enough capital, such that their probability of becoming insolvent over a fixed time horizon (e.g. 1 year) is very low (e.g. at most 0.5%). Calculation of the required capital according to this principle stumbles on the quite fundamental difficulty of estimating the probability of very extreme scenarios based on limited data sets. In particular, the estimated capital / VaR values may in fact be different - higher or lower - than what they should be.
For any given institution it is not possible to say whether the estimated capital is more or less than its required level. We can, however, examine the extent to which the insolvency probability of an institution is affected by parameter uncertainty. In particular, a regulator is interested in the percentage of regulated insurance companies that would be expected to default in a given year. We show that for a range of simple loss models, including the popular Pareto, Lognormal and Weibull models, we can calculate such insolvency probabilities explicitly, even if the true model parameters remain unknown.
In figure 1 we give an illustration of such calculations. We assume that capital is calculated according to a regulatory requirement of a 0.5% probability of insolvency; this can be adjusted to reflect higher rating targets. Then we plot the actual insolvency probability, when taking into account the effect of parameter uncertainty. Insolvency probabilities are plotted for the Lognormal and Pareto models (vertical axis), against the number of data from which capital was estimated (horizontal axis). We observe that:
- For both models the probability of insolvency is larger than the required level of 0.5%, hence parameter uncertainty has a detrimental effect on capital adequacy.
- For small data sets the insolvency probability become much higher than the required level of 0.5%, while for larger data sets the insolvency probability reduces towards its required level. This shows that the effect of parameter uncertainty is greatest when less information about the modelled risks is available.
- The insolvency probabilities are larger for the Lognormal model. This is in spite of the Pareto model being more "heavy-tailed", that is, corresponding to a loss profile more likely to produce extreme losses. Of more importance seems to be the number of parameters to be estimated in each case: 2 for the Lognormal and 1 for the Pareto model. This indicates that model complexity may amplify the effect of parameter uncertainty.
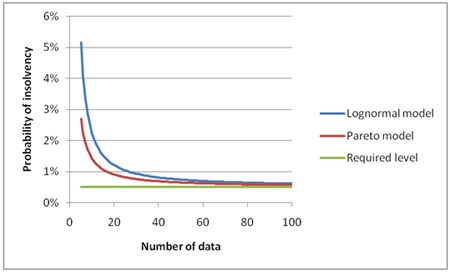
Figure 1: Insolvency probabilities for the Lognormal and Pareto loss models, as functions of the size of the data set used in capital estimation.
So what should be done? One solution would be to require companies with short experience to hold more capital, by making the VaR confidence level dependent on the size of the dataset used in the capital calculation. However such an approach, apart from being politically unenforceable, would fly in the face of principles-based regulation such as ICAS and Solvency II.
Fortunately a better alternative exists. A company can reflect parameter uncertainty within its own calculations by modifying the loss model itself. The most established way of doing this is via Bayesian arguments. Using such methods, capital is calculated according to a predictive distribution, which reflects both the risk of losses and the parameter risk. A smaller data set will produce a predictive distribution that leads to a higher capital requirement and thus parameter uncertainty will be implicitly reflected.
Would such an approach work from the point of view of a regulator? The answer is yes. We prove in our paper that for the class of loss models considered, the use of a predictive distribution for capital calculations would make the insolvency probability of each company the same, even allowing for parameter uncertainty. Hence, the regulator would succeed in establishing a minimum level of policyholder security that is both adequate and uniform across firms. Moreover, such an approach would not require an over-prescriptive or intrusive approach by regulators. Adopting a predictive distribution for capital calculation would amount to a modification of the solvency standard itself, which would then be enforced consistently across the sector.
|


